The binding energies of single ionized Helium are given by
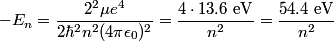 where 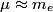 is the reduced mass. is the reduced mass.The energy of the photon is 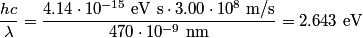 Thus, 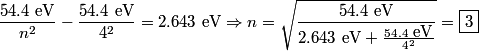 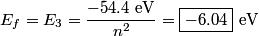 Therefore, answer (A) is correct. |
The binding energies of single ionized Helium are given by
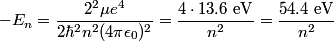 where 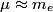 is the reduced mass. is the reduced mass.The energy of the photon is 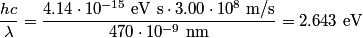 Thus, 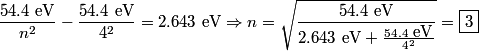 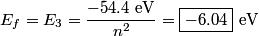 Therefore, answer (A) is correct. |